Writing ourselves an Zstandard codec in Rust. Part X.
Disclaimer: this is not final. If you find mistakes, please report them.
Part X: Preparing for compression
This post is part of a series on entropy coding and writing our own Zstandard library in Rust.
Part I · II · III · IV · V · VI · VII · VIII · IX · X
We need to lay some groundwork to tackle compression. Our concern is that decompression is well-defined, meaning that from a (valid) input you can only reasonably provide one output. Indeed we have a checksum for that.
Compression, however, is not so: you may compress a file in many different ways, which will all decompress correctly. As you may remember, each block may be stored uncompressed, or compressed using RLE, of using tANS/FSE, with or without explicit frequency tables, which themselves are to an extent free to choose. The compressor has to make the right calls, decide which is best for each block, according to some metric.
In general, the relevant metric is compressed size: we want the compressed file to be as short as possible. But we could come up with other metrics: faster compression (less work for the compressor), faster decompression (less work for the decompressor), compatibility with such or such implementation (e.g., refrain from using some compression type), etc.
Oh, did I mention that it’s up to the compressor to decide how large blocks are? That’s right, it’s not just picking the best our of a few options, it’s also slicing the input in the best way possible.
Fig. 1: Block splitting.
Compressors typically try to answer these questions by a combination of heuristics and optimization techniques. This is what we discuss here.
Small disclaimer: exceptionally, there isn’t any Rust in this post. Sorry about that.
Block splitting and the case of RLE
Say we are given some input data. We can split this data into blocks, with the following constraints:
- Blocks shouldn’t overlap, and each bit of the input data ends up belonging to some block (this is a set partition)
- Creating a block has a fixed cost \(C\) (in bits), plus a variable cost that depends on its contents
Namely,
- If the block is uncompressed, its variable cost equals the length of its contents (in bits)
- If the block is RLE-compressed, its variable cost is zero
- If the block is compressed, its variable cost equals its contents Shannon entropy
This is a simplified model, but it will be more than sufficient to highlight the difficulties and strategies that one can apply. We’ll throw away this entropy thing at the end of this post anway.
Our goal is to find the block decomposition of our input that minimizes the total cost, defined as the sum of the blocks’ cost.
If we’re only allowing uncompressed blocks, the optimal solution is to have a single block, with total cost = \(C\) + length of input data. Indeed, any additional block adds \(C\) to this value, with no benefit.
For the problem to be non-trivial, we must consider at least another type of blocks, say RLE-compressed blocks. Not all data can be RLE in Zstandard: only repeating symbols. But when we encounter say \(r\) repeating bytes, we can decide to create a dedicated RLE block for them or not. This is interesting as soon as \(8r > 2C\), and there is no real drawback.
Why \(2C\) and not just \(C\)? In general, when we create one RLE block in the middle, that means there is a block before and a block after: so what previously was one contiguous uncompressed block becomes 3 blocks. In corner cases, you don’t create this additional block (try to find them these cases for yourself). For simplicity, we won’t chase this minor optimization here.
We can scan the input linearly, look for runs that are long enough, and when they are, create an RLE block for them. Here’s a Python pseudo-code:
data = 'testdaaaaatateeeeestt'
blocks = []
prev = None
start = 0
C = 10
for (pos, symbol) in enumerate(data):
if symbol != prev:
# End of a run
length = pos - start
if length * 8 > 2 * C:
# The run is long enough
blocks.append(("RLE", prev, start, length))
prev = symbol
start = pos
print(blocks)
# > [('RLE', 'a', 5, 5), ('RLE', 'e', 13, 5)]
With that out of the way, our initial data is partitioned between RLE blocks, which we won’t have to deal with any further, and “the rest”.
An experiment
Uncompressed blocks have a cost that is easy to understand; compressed blocks, however, are harder to grasp because their cost is non-linear. We assumed that entropy was the appropriate measure of the “cost” when performing compression: this is a very crude estimate, and shouldn’t be taken at face value. It only acts as a heuristic. Still, we need to understand this heuristic.
Let’s work on an example. Our input data will be the first bytes of /bin/sh. This is just a picture, but it will give some intuition.
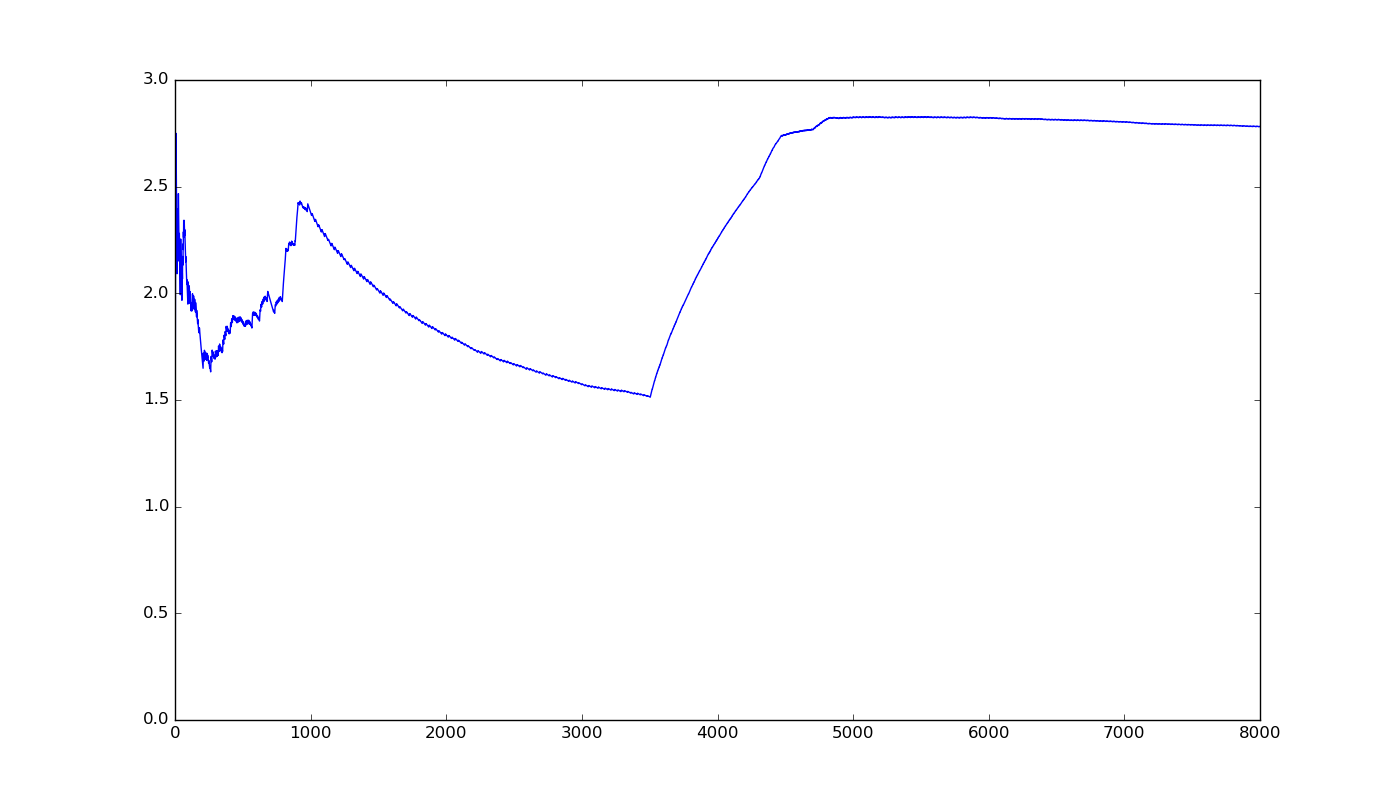
The above picture considers the per-symbol entropy of data[0:i] as i moves from 1 to about 8000.
Observe that per-symbol entropy does not follow a simple, obvious pattern; rather it displays many large fluctuations. It is neither convex nor concave and there doesn’t seem to be a way to predict its behaviour.
If we were to compress the entire 8000-byte sequence in a single block, it would require about 23000 bits: 8000 times the per-symbol entropy of ̀data[0:8000]. But what if we split the input into two blocks, say in the middle?
- The per-symbol entropy of
data[0:4000]is \(2.254\) - The per-symbol entropy of
data[4001:8000]is \(3.086\)
Which correspond to blocks of respective size \(2.54 \times 4000 = 9017.5\) and \(3.086 \times 4000 = 12345\) — totalling 21362 bits; which is almost 2000 bits shorter than using a single block.
We don’t have to split exactly in the middle, we can look at what happens when we move the separation around. On this graph the x-axis represents the position of the split between blocks:
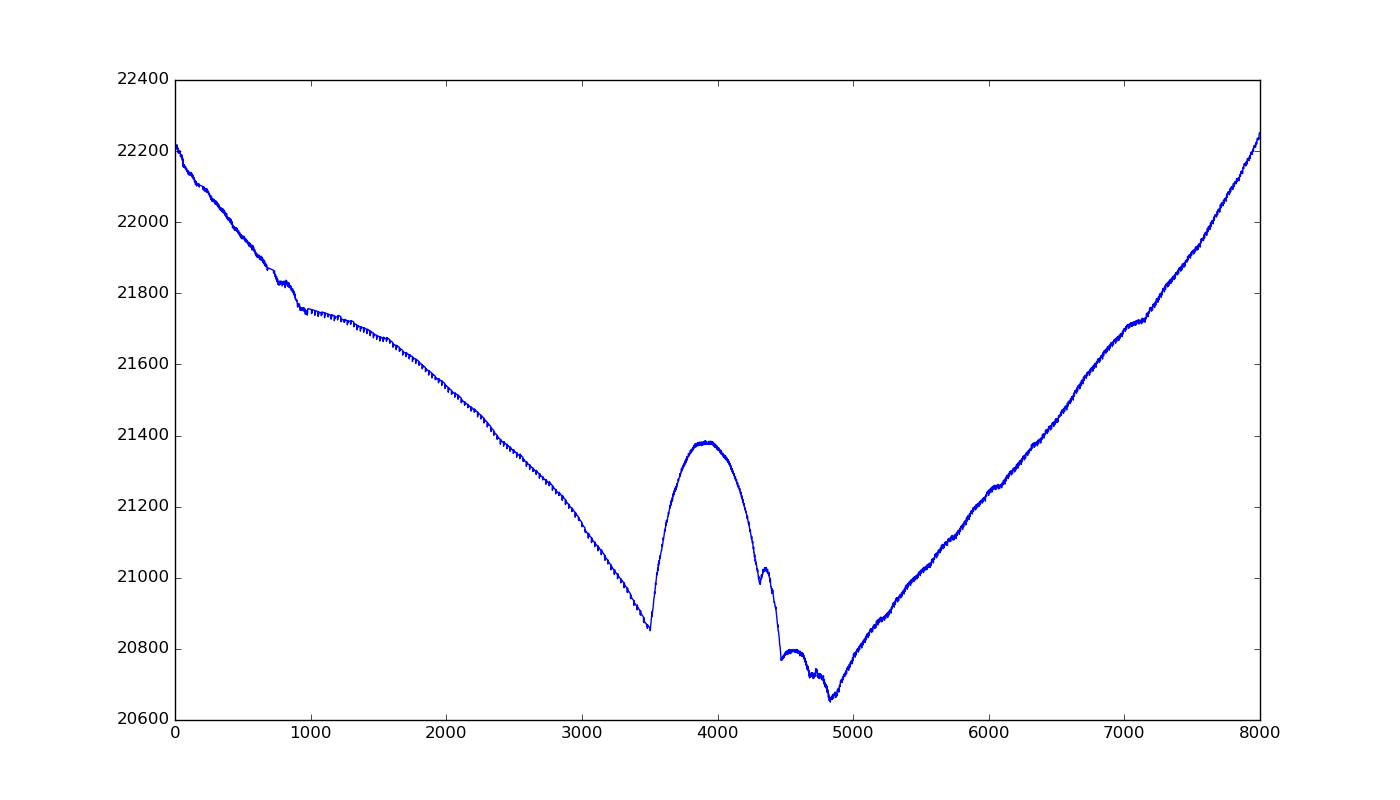
The best solution here, corresponding to the minimum on the graph above, is to split at position 4832, resulting in a total cost of 20651. But, wait! If two blocks make things better, why not try three blocks?
What about several blocks?
Testing all pairs of indices in a sequence of length \(n\) makes \(O(n^2)\) calls to the test function, and computing entropy is linear time, so overall finding the best three-block partition by our method takes something like \(O(n^3)\). For \(n \approx 8000\) this is already pushing our limits.
Alternatively, we can try to take our 2-block partition from above, and split each block in half. Recursively splitting blocks yields interesting results:
- 1 compressed block: 22252 bits (reference) (stops: none)
- 2 compressed blocks: 20651 bits (-7%) (stops: 4832)
- 4 compressed blocks: 18595 bits (-18%) (stops: 3504, 4832, 6383)
- 8 compressed blocks: 16687 bits (-25%) (stops: 975, 3504, 4470, 4832, 5759, 6383, 7151)
- 16 compressed blocks: 15724 bits (-29%) (stops: 791, 975, 2303, 3504, 4308, 4470, 4691, 4832, 5255, 5759, 6095, 6383, 6671, 7151, 7559)
This recursive algorithm is not optimal, but it is tractable.
It would seem that increasing the number of blocks improves compression, but we haven’t accounted for the constant overhead cost of creating a block. This cost is small compared to our gains, but it compounds.
On paper, accounting for the overhead, we don’t want to exceed \(nS/C\) where \(S\) is the per-symbol entropy of the full input. Using more blocks than this value will inevitably make things worse.
The bottom-up approach
There are several limitations to the approach discussed so far. One of them is that we need to parse the entire input before we can decide how to split it. We even end up reading every symbol multiple times as part of this procedure. Furthermore, we may end up with many small blocks.
Many small blocks may look appealing from an entropy standpoint, even accounting for the overhead, but they are annoying to deal with. Indeed, most of the processing time would be spent dealing with block headers, which is metadata rather than data itself. What’s worse, small blocks render dictionary compression useless; repetition needs space.
Instead of taking the whole input, and then splitting it, we may start with smaller units and build up blocks by merging them. To that effect, we’ll read the input once:
- All RLE blocks will be identifed
- All that isn’t an RLE block will be split into (approximately) fixed-size windows
Importantly, we do not need to scan the entire input ( which means we can apply this to a stream of data and compress on the fly, although that isn’t our goal here).
Fig. 2: Initial scan. RLE blocks have been removed for clarity.
The entropy of two windows is lower or equal than the sum of each window’s entropy. This leads to the following idea of an algorithm:
- Prepare a current empty block
- Compute the entropy of the next window
- If the window entropy exceeds a certain threshold \(\tau\), we won’t try to compress this window: if the current block is (empty or) “uncompressed”, merge the window into it. Otherwise if the current block is “compressed”, create a new “uncompressed” current block from the current window. Goto 2.
- If the current block is “uncompressed” then create a new “compressed” block from the current window. Goto 2.
- (Reaching this step, the current block is “compressed”, non empty, and the current window has an entropy below the threshold) Append this window to the current block. Goto 2.
Once this attribution has been made, we can go on actually performing the compression or not, and we’ll be done.
The block splitting algorithm (in Python)
RLE = 0
COMP = 1
UNCOMP = 2
blocks = []
windows = []
cur_win = []
cur_block_type = UNCOMP
prev = None
start = 0
last = 0
C = 10
W = 20
tau = 15
for (pos, symbol) in enumerate(data):
cur_win.append(symbol)
# This saves us from one identation level
if symbol == prev:
continue
# End of an RLE run
length = pos - start
if length * 8 > 2 * C:
# The run is long enough
blocks.append([RLE, prev, length])
cur_block_type = RLE
last = pos - 1
cur_win = [symbol]
else:
# The run isn't long enough: RLE ruled out
# One window complete
if pos - last = W:
win_entropy = entropy(cur_win)
if win_entropy > tau:
# We won't compress
if cur_block_type == UNCOMP:
# Merge with current block
blocks[-1][-1] += cur_win
else:
# Create new block
blocks.append([UNCOMP, cur_win[:]])
cur_block_type = UNCOMP
else:
# We will compress
if cur_block_type == COMP:
# Merge with current block
blocks[-1][-1] += cur_win
else:
# Create new block
blocks.append([COMP, cur_win[:]])
cur_block_type == COMP
last = pos
cur_win = []
prev = symbol
start = pos
On the plus side, this algorithm only reads the input once, and can easily be adjusted to process data in a streaming fashion.
On the minus side, the resulting compression is less impressive, in no small part because we made the worst-case assumption that entropy adds up (when, in reality, it could go down).
Now, throughout this post, we’ve used entropy as a proxy for how well compression would perform. This is not a very good metric, as we’ve had the opportunity to discuss. If our compressor is fast (which hopefully it will be) instead of computing entropy, we can compress the window and check its actual size. This will give more accurate results. And in some cases this is exactly what we need to do anyway.
Conclusion
At the end of this post, we have an algorithm that takes the input and determines how it should be split into blocks, as well as the compression method to apply to these blocks. We traded compression strength for the ability to read the input as a stream, an keep complexity linear.
In the next post, we’ll translate this algorithm into Rust and put it to good use, as this should be the first steps of our Zstandard compressor. Stay tuned!
Did you like this? Do you want to support this kind of stuff? Please share around. You can also buy me a coffee.